Publications

2023

• Tara LaForce, Eduardo Basurto, Lisa Bigler, Kyung W. Chang, Mohamed Ebeida, Richard Jayne, Rosie Leone, Paul Mariner, Jeff Sharpe. GDSA Repository Systems Analysis Investigations in FY 2023

This report describes specific activities in the Fiscal Year (FY) 2023 associated with the Geologic Disposal Safety Assessment (GDSA) Repository Systems Analysis (RSA) work package funded by the Spent Fuel and Waste Science and Technology (SFWST) Campaign of the U.S. Department of Energy Office of Nuclear Energy (DOE-NE), Office of Spent Fuel and Waste Disposition (SFWD).

• Lisa Bigler, Tara LaForce, Eduardo Basurto. Incorporating Geological Structure into Sensitivity Analysis of Contaminant Transport Modeling

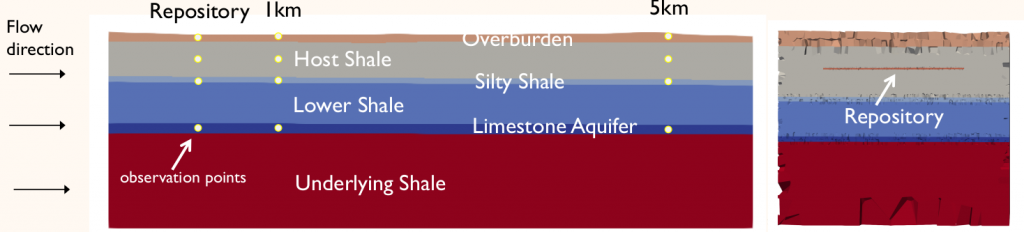
Simulating subsurface contaminant transport at the kilometer-scale often entails modeling reactive flow and transport within and through complex geological structures. These structures are difficult to mesh and as a result geologic structure is typically represented by one or a few deterministically generated meshes for uncertainty studies. Uncertainty in geologic structure can have a significant impact on contaminant transport and should be fully incorporated within uncertainty quantification (UQ) and sensitivity analysis (SA) for subsurface contaminant modeling.

• Tara LaForce, Lisa Bigler, Kristopher Kuhlman, Michael Nole. Voronoi or Hexahedral Meshing for Simulation Accuracy and Speed

In simulations of fluid flow through porous media it is frequently necessary to flex meshes to conform to geological features. However, the poor quality of the resulting mesh can negatively impact the accuracy of the simulation. Structured meshes can also systematically bias the calculated flow field. One alternative is to simulate using unstructured Voronoi meshes. Voronoi meshes have orthogonal fluxes between cells, and unstructured meshes do not bias the flow field, reducing two sources of numerical error. Unfortunately, simulating on unstructured polyhedral meshes can significantly increase simulation time. A series of analytical benchmark problems are simulated on three-dimensional hexahedral, flexed-hexahedral, and Voronoi meshes using the finite volume simulator PFLOTRAN. The accuracy of simulated results and computation times are compared. Finally, simulations of experiments of unstable two-phase flow are compared.

2022

• Tara LaForce, Mohamed Ebeida, Spencer Jordan, Terry A. Miller, Philip H. Stauffer, Heeho Park, Rosie Leone, Glenn Hammond. Voronoi Meshing to Accurately Capture Geological Structure in Subsurface Simulations https://doi.org/10.1007/s11004-022-10025-x . October 12^th, 2022

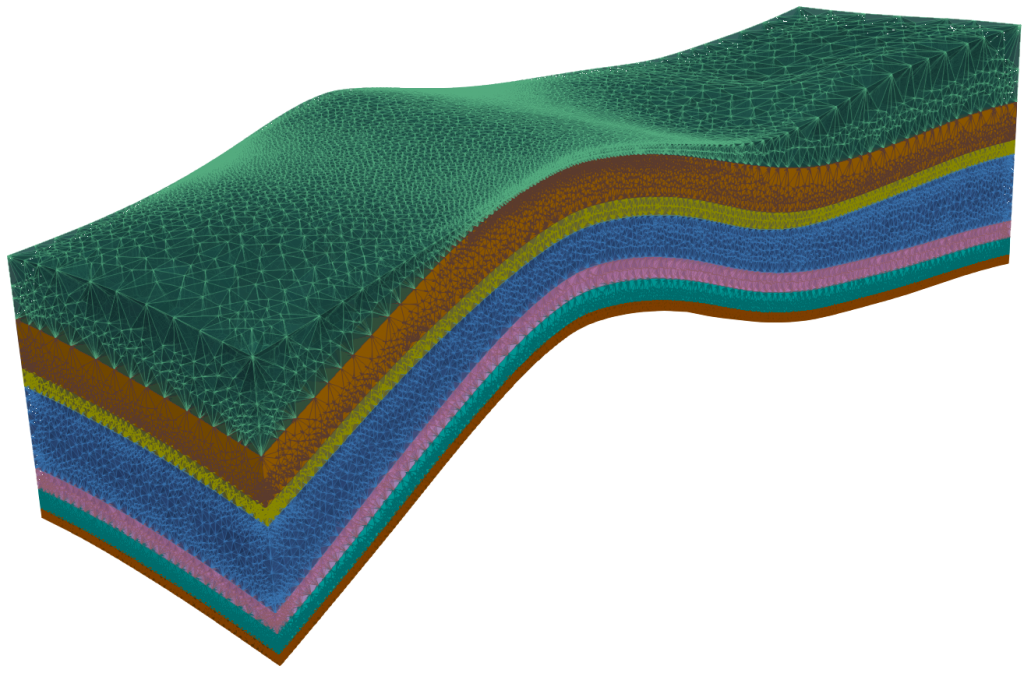
Mesh generation lies at the interface of geological modeling and reservoir simulation. Highly skewed or very small grid cells may be necessary to accurately capture the geometry of geological features, but the resulting poorly scaled or small grid cells can have a substantial negative impact on simulator accuracy and speed. One way to minimize numerical errors caused by gridding complex structures is to simulate on high-quality Voronoi meshes, which reduce grid orientation effects in fluid flow. This work presents a complete methodology to create Voronoi simulation grids, model fluid flow in complex geological systems, and visualize the results. A recently developed Voronoi meshing method that can automatically generate provably good unstructured meshes that conform to input surfaces creating closed volumes is used. Initially an analytical benchmark simulation is presented to validate the quality of the meshes and simulation results and demonstrate the superiority of simulation results using Voronoi meshes over flexed-hexahedral meshes on a domain with internal features. Next, meshes are created for test structures representing four of the most common geological features in the subsurface: layering, pinch-out, an interior lens that tapers to zero thickness on all sides and a fault with offset. Two benchmark flow simulations are run for each test structure. Finally, a realistic geological example for CO2 injection into an anticline is simulated. Three realizations of the Voronoi mesh at the same resolution are generated for the simulations. Each mesh is highly refined near the injection wells and coarse in areas of less interest. These three meshes are used to model the CO2 plume in the subsurface as it migrates to the top of the structure and then fills downward. Simulations on the meshes with randomly generated elements inside the input volumes each give slightly different fingering patterns for the viscous-unstable buoyant gas flow. The results presented in this work show a promising step towards utilizing fully automated Voronoi meshing for subsurface flow simulations in complex geology.

2020

• Mohamed S. Ebeida. Constructing a conforming Voronoi mesh for an arbitrarily-shaped enclosed geometric domain.
  United States Patent #10,776,540. September 15, 2020.
  
  A computing system is described herein, where the computing system includes a processor and memory storing instructions that, when executed by the processor, cause the processor to perform the following acts: 1) receiving a computer-implemented definition of an enclosed geometric domain, wherein the geometric domain is three-dimensional; 2) determining locations of seeds for the enclosed geometric domain; 3) decomposing the enclosed geometric domain into a conforming Voronoi mesh based on the locations of the seeds, wherein the conforming Voronoi mesh comprises Voronoi cells, and further wherein the conforming Voronoi mesh is bounded by the enclosed domain; and 4) performing a numerical simulation to generate simulation results, wherein the numerical simulation is based on at least one Voronoi cell in the Voronoi cells of the conforming Voronoi mesh.
  
  

• Mohamed S. Ebeida. Constructing a conforming Voronoi mesh for an arbitrarily-shaped enclosed geometric domain.
  United States Patent #10,776,537. September 15, 2020.
  
  A computing system is described herein, where the computing system includes a processor and memory storing instructions that, when executed by the processor, cause the processor to perform the following acts: 1) receiving a computer-implemented definition of an enclosed geometric domain, wherein the geometric domain is two-dimensional; 2) determining locations of seeds for the enclosed geometric domain; 3) decomposing the enclosed geometric domain into a conforming Voronoi mesh based on the locations of the seeds, wherein the conforming Voronoi mesh comprises Voronoi cells, and further wherein the conforming Voronoi mesh is bounded by the enclosed domain; and 4) performing a numerical simulation to generate simulation results, wherein the numerical simulation is based on at least one Voronoi cell in the Voronoi cells of the conforming Voronoi mesh.
  
  

• Ahmed Abdelkader, Chandrajit L. Bajaj, Mohamed S. Ebeida, Ahmed H. Mahmoud, Scott A. Mitchell, John D. Owens, and Ahmad A. Rushdi. 2020. VoroCrust: Voronoi Meshing Without Clipping. ACM Trans. Graph. 39, 3, Article 23 (May 2020), 16 pages.
  https://doi.org/10.1145/3337680
  
  Polyhedral meshes are increasingly becoming an attractive option with particular advantages over traditional meshes for certain applications.
  
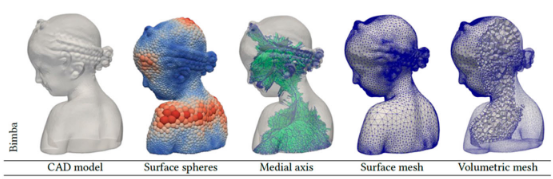
  What has been missing is a robust polyhedral meshing algorithm that can handle broad classes of domains exhibiting arbitrarily curved boundaries and sharp features. In addition, the power of primal-dual mesh pairs, exemplified by Voronoi-Delaunay meshes, has been recognized as an important ingredient in numerous formulations. The VoroCrust algorithm is the first provably correct algorithm for conforming polyhedral Voronoi meshing for non-convex and non-manifold domains with guarantees on the quality of both surface and volume elements. A robust refinement process estimates a suitable sizing field that enables the careful placement of Voronoi seeds across the surface, circumventing the need for clipping and avoiding its many drawbacks. The algorithm has the flexibility of filling the interior by either structured or random samples while preserving all sharp features in the output mesh. We demonstrate the capabilities of the algorithm on a variety of models and compare against state-of-the-art polyhedral meshing methods based on clipped Voronoi cells establishing the clear advantage of VoroCrust output.
  • High Resolution Paper PDF: Click here
  • Supplemental Materials: Click here

2019

• Mohamed S. Ebeida. Generating an implicit Voronoi mesh to decompose a domain of arbitrarily many dimensions.
  United States Patent #10,304,243. May 29, 2019.
  
  Described herein are technologies pertaining to generating a Voronoi mesh for an enclosed domain of arbitrarily many dimensions. An implicit Voronoi mesh is received that comprises locations of seeds in the domain. Neighbors of a seed are identified by extending a segment from the seed to the boundary of the domain and performing successive hyperplane trimming of the segment to identify a point on the facet of the Voronoi cell of the seed. A vertex of the cell can be identified by successively extending and trimming one or more additional spokes to identify points on a facet of the cell that are constrained to lie in a (d-n) space, where d is a number of dimensions of the domain and n is a number of iterations. A numerical simulation is performed based on the Voronoi mesh to generate simulation results in applications including surrogate modeling, global optimization, calibration, dimension reduction.

2018

• Abdelkader, A., Bajaj, C. L., Ebeida, M. S., Mahmoud, A. H., Mitchell, S. A., Rushdi, A. A., & Owens, J. D. (2018). Sampling Conditions for Conforming Voronoi Meshing by the VoroCrust Algorithm. LIPIcs : Leibniz International Proceedings in Informatics, 99, 10.4230/LIPIcs.SoCG.2018.1.
  https://doi.org/10.4230/LIPIcs.SoCG.2018.1
  
  We study the problem of decomposing a volume bounded by a smooth surface into a collection of Voronoi cells. Unlike the dual problem of conforming Delaunay meshing, a principled solution to this problem for generic smooth surfaces remained elusive. VoroCrust leverages ideas from alpha-shapes and the power crust algorithm to produce unweighted Voronoi cells conforming to the surface, yielding the first provably-correct algorithm for this problem. Given an epsilon-sample on the bounding surface, with a weak sigma-sparsity condition, we work with the balls of radius delta times the local feature size centered at each sample. The corners of this union of balls are the Voronoi sites, on both sides of the surface. The facets common to cells on opposite sides reconstruct the surface. For appropriate values of epsilon, sigma and delta, we prove that the surface reconstruction is isotopic to the bounding surface. With the surface protected, the enclosed volume can be further decomposed into an isotopic volume mesh of fat Voronoi cells by generating a bounded number of sites in its interior. Compared to state-of-the-art methods based on clipping, VoroCrust cells are full Voronoi cells, with convexity and fatness guarantees. Compared to the power crust algorithm, VoroCrust cells are not filtered, are unweighted, and offer greater flexibility in meshing the enclosed volume by either structured grids or random samples.