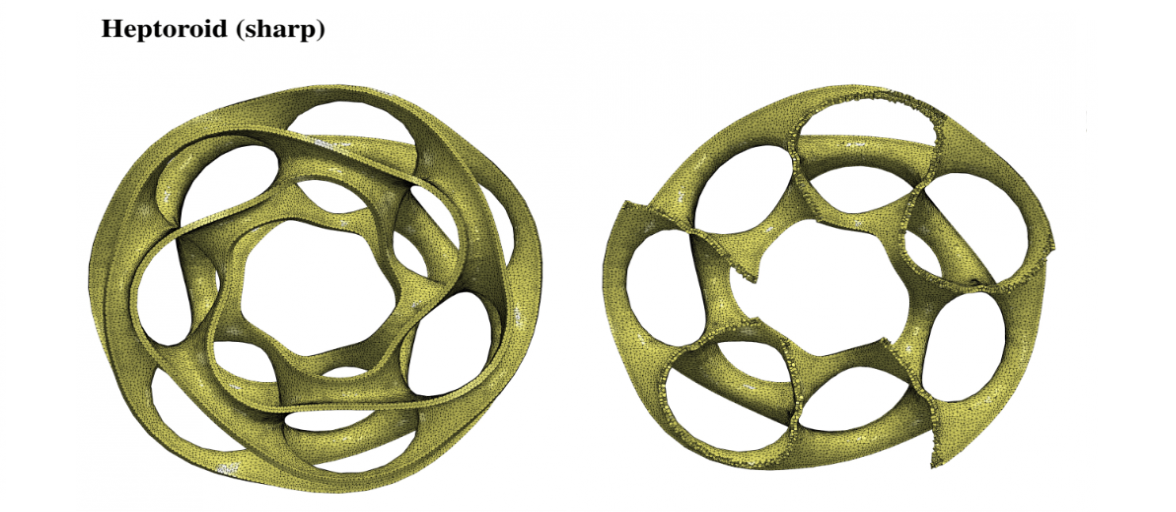VoroCrust

VoroCrust is the first provably correct algorithm for conforming Voronoi meshing of non-convex and non-manifold domains
VoroCrust 3D renderings

3D Rendering of a triceratops

3D Rendering of a gear

3D Rendering of a chazelle

3D Rendering of a rocker arm exhaust

3D Rendering of Otomondo

3D Rendering of spaghetti

3D Rendering of a loop

3D Rendering of a Heptroid

3D Rendering of a goat

3D Rendering of a fertility figurine

3D Rendering of an elephant

3D Rendering of a Chinese dragon

3D Rendering of a closed hand

3D Rendering of an open hand

3D Rendering of statue of David's head

3D Rendering of bimba

3D Rendering of close Hemispheres

VoroCrust 3D renderings collection

VoroCrust

VoroCrust is the first provably correct algorithm for conforming Voronoi meshing of non-convex and non-manifold domains with guarantees on the quality of both surface and volume elements.

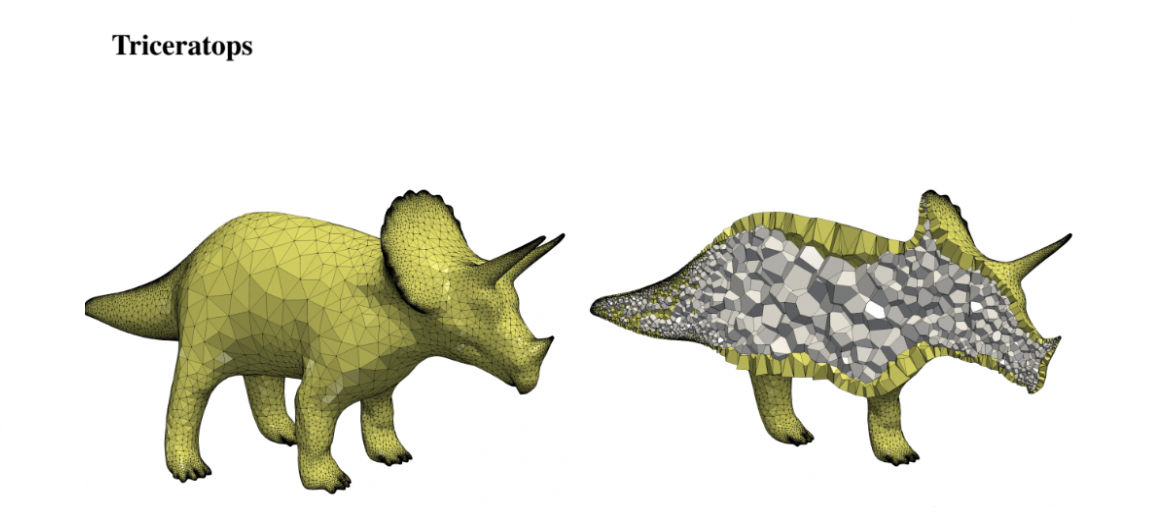
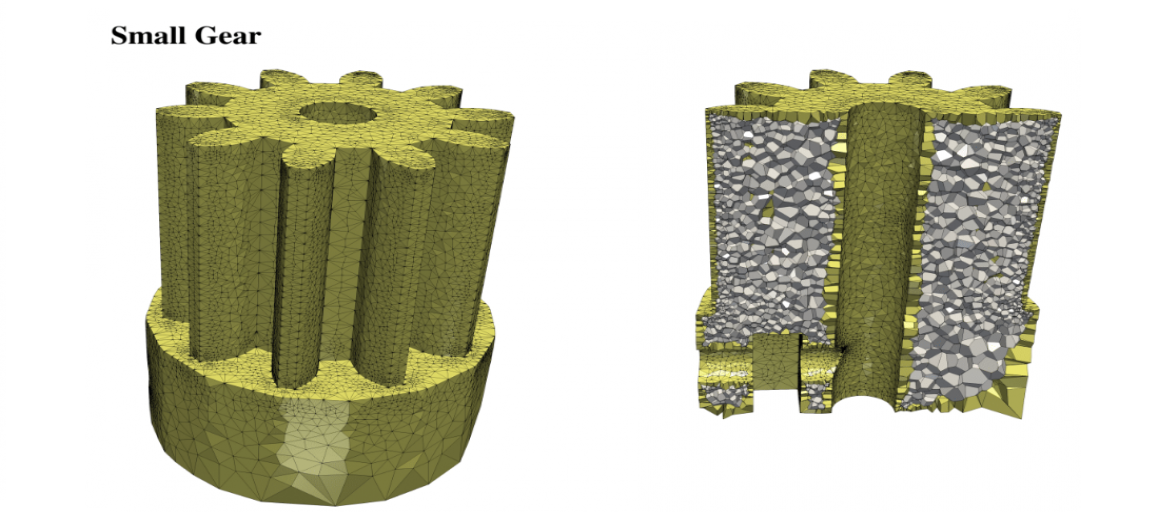
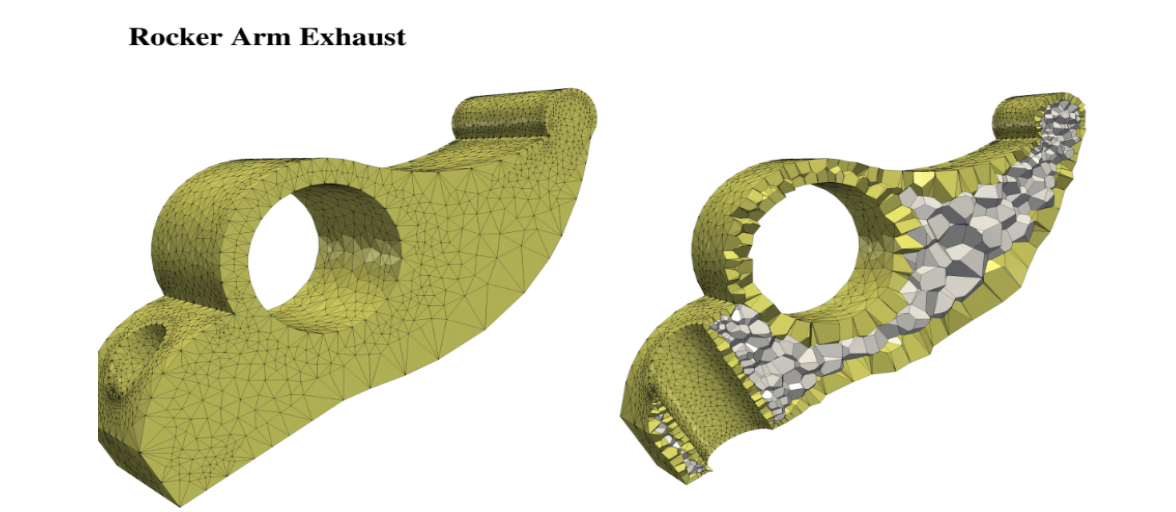
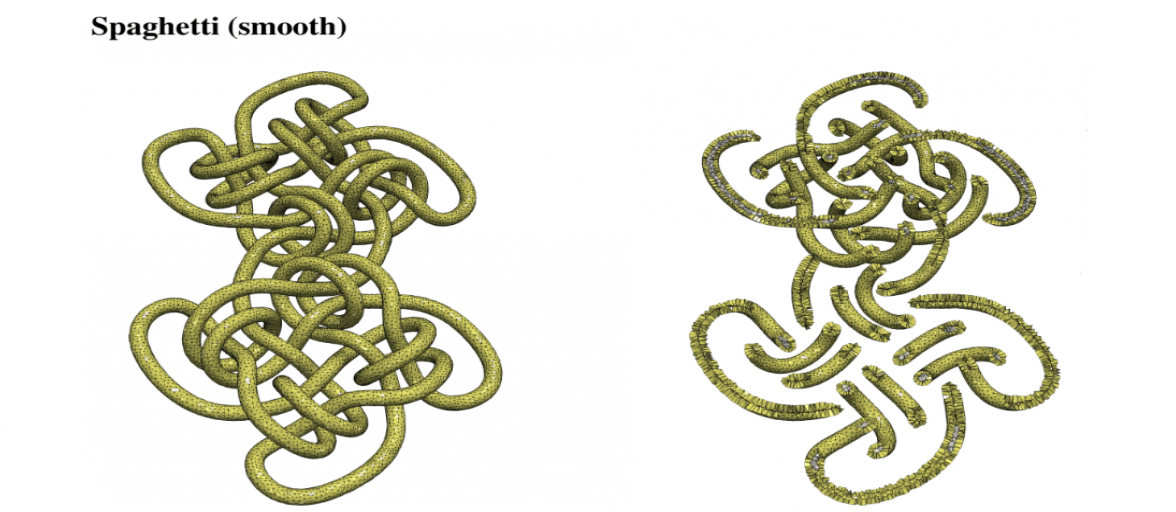
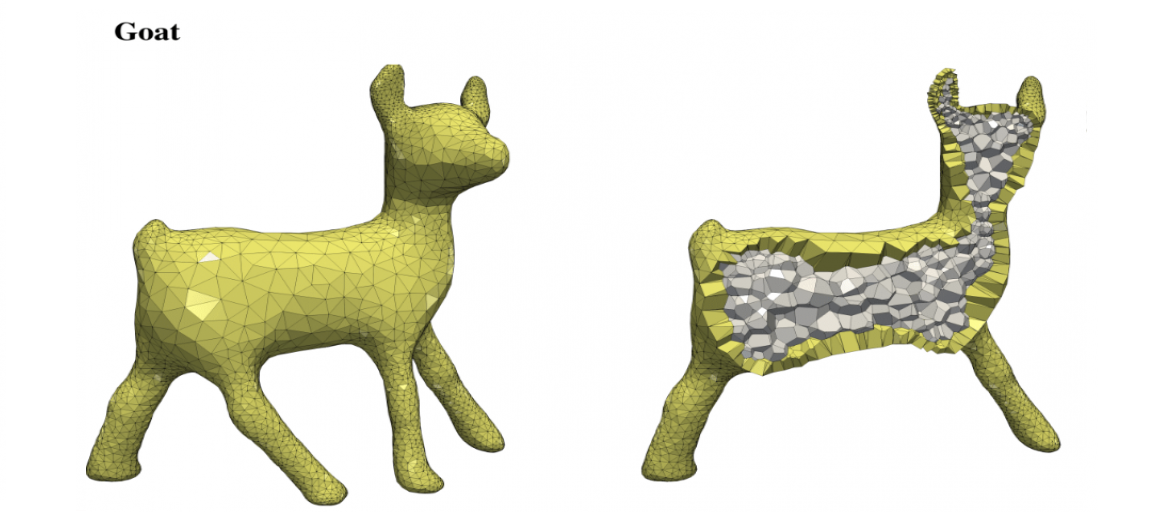
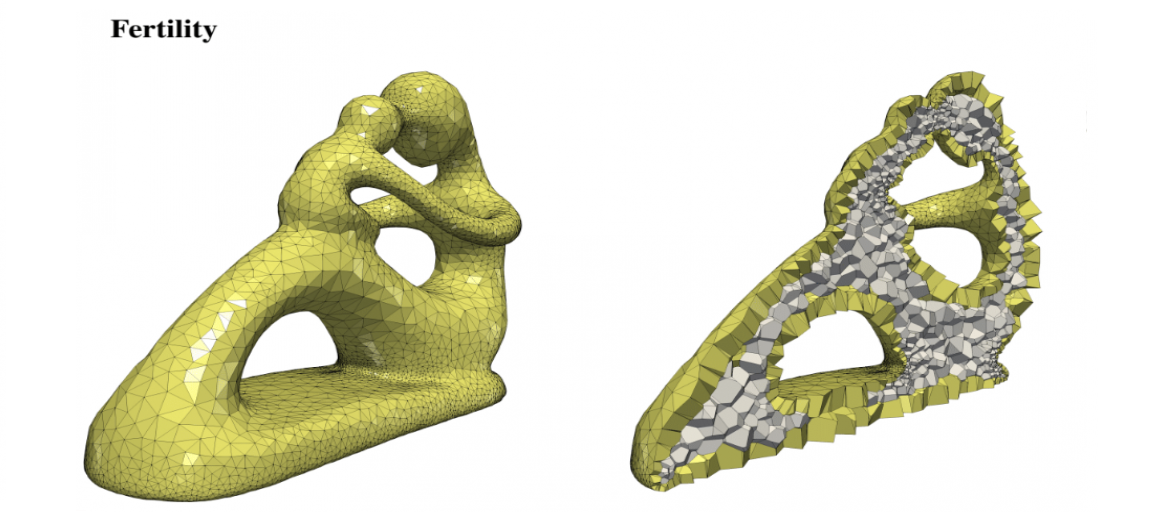
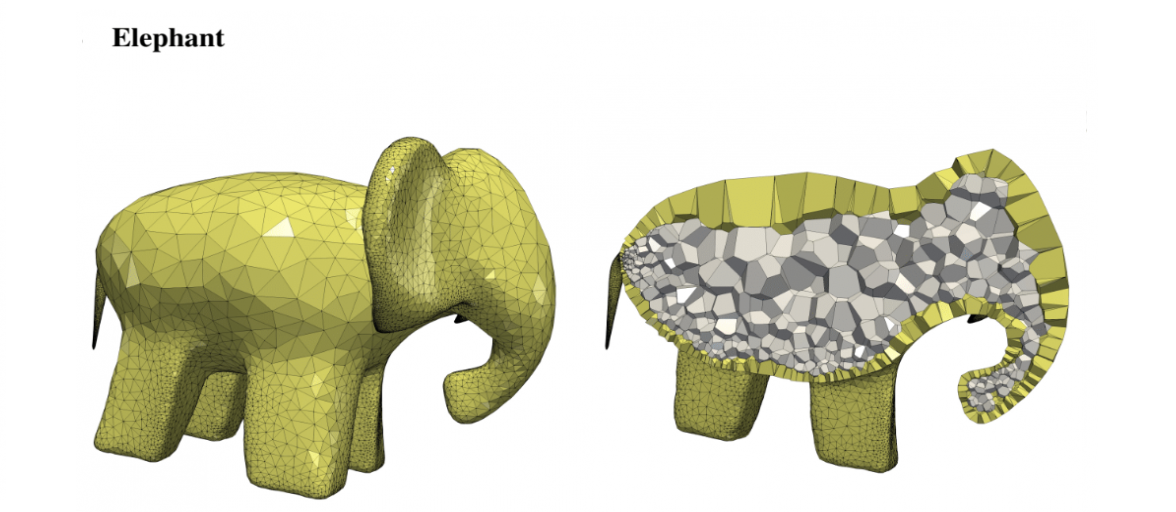
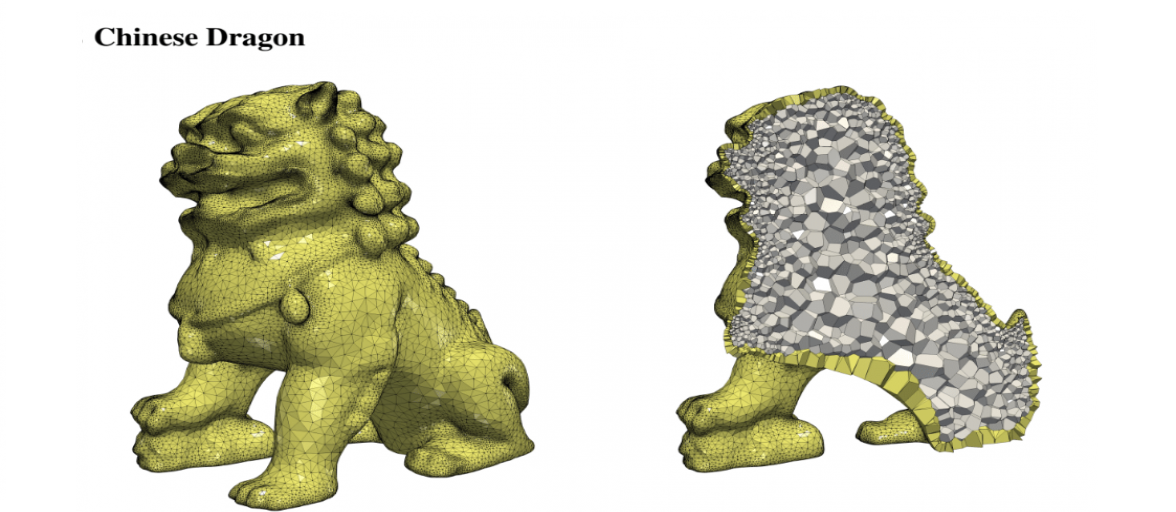
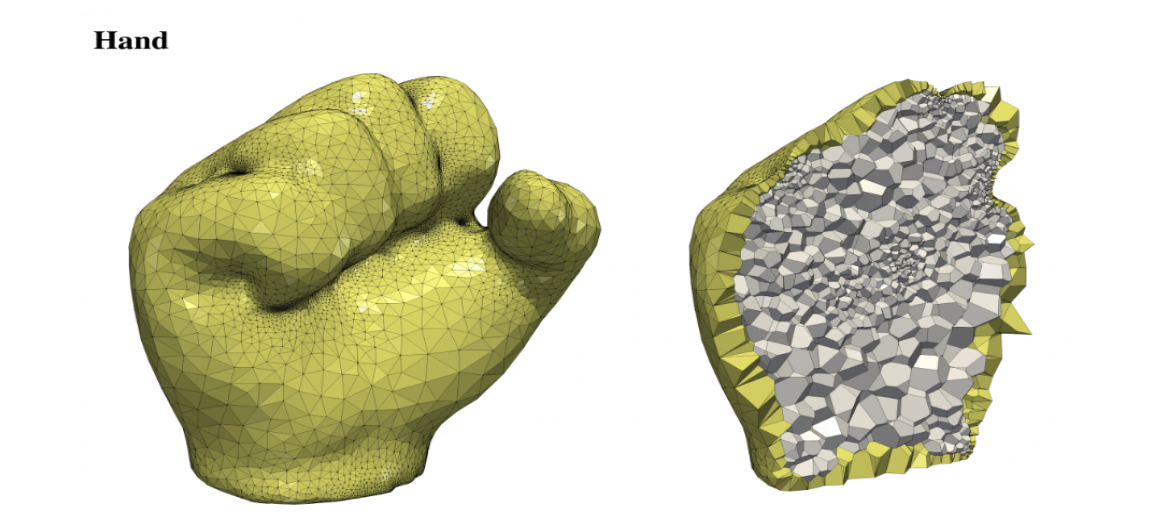
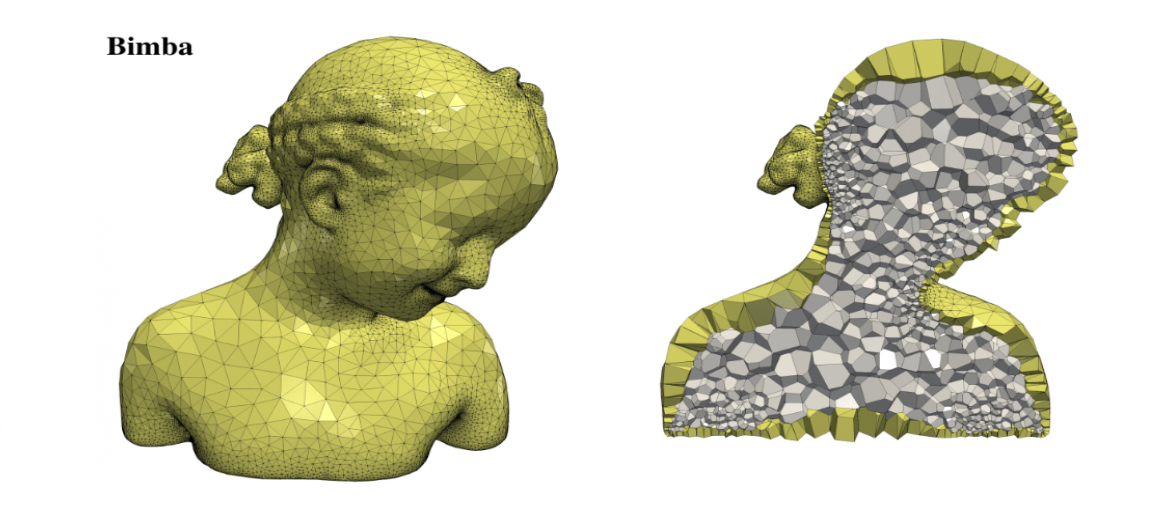
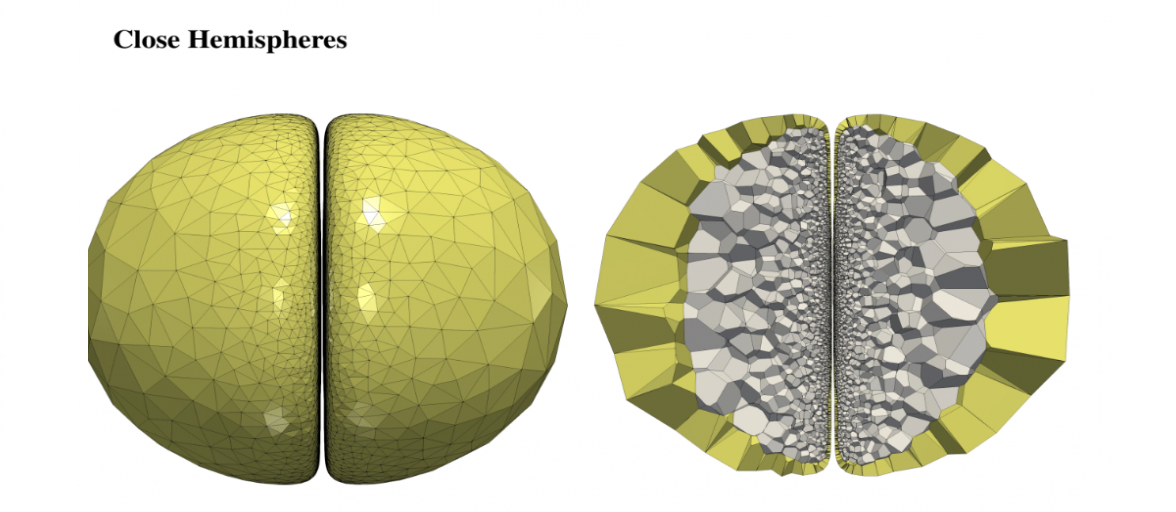
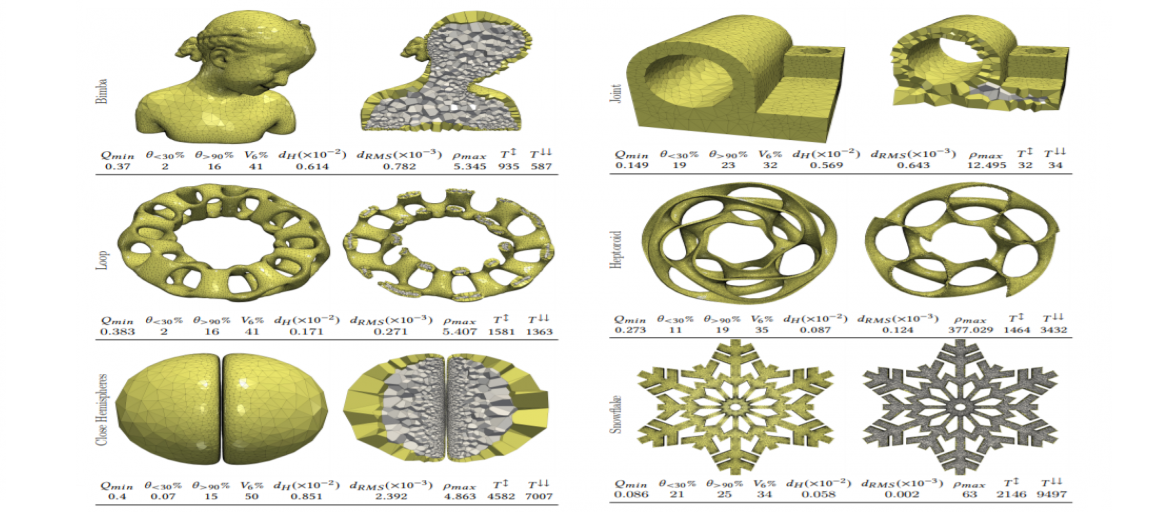
Polyhedral meshes are increasingly becoming an attractive option with particular advantages over traditional meshes for certain applications. What has been missing is a robust polyhedral meshing algorithm that can handle broad classes of domains exhibiting arbitrary curved boundaries and sharp features. In addition, the power of primal-dual mesh pairs, exemplified by Voronoi-Delaunay meshes, has been recognized as an important ingredient in numerous formulations. Vorocrust deploys a robust refinement process to estimate a suitable sizing field that enables the careful placement of Voronoi seeds across the surface circumventing the need for clipping and avoiding its many drawbacks. The algorithm has the flexibility of filling the interior by either structured or random samples, while all sharp features are preserved in the output mesh. We demonstrate the capabilities of the algorithm on a variety of models and compare against state-of-the-art polyhedral meshing methods based on clipped Voronoi cells establishing the clear advantage of VoroCrust output. 

VoroCrust has attracted the attention of Earth Scientists at Sandia and Los Alamos National Laboratories due to its unique capabilities.  SNL is incorporating VoroCrust into a framework for simulation of deep geologic repositories for nuclear waste. A LANL geoscience webpage states: “Polyhedral meshing is important for flow and transport codes which include TOUGH2, FEHM, PFLOTRAN, and MODFLOW which are based on the two-point flux discretization. While the solution to flow/transport is stable without an orthogonal mesh, it is not accurate. Geometry conforming Voronoi tessellations are difficult to produce if the geometry is complex. So, if you want orthogonal discretization and you want complex geometry, you need conforming Voronoi tessellations.”

The VoroCrust software is owned by Sandia National Laboratories.

To obtain the code, download from here. In addition you can download from source via our public Github page: Coming Soon